CHAPTER 7

Arithmetic coding procedure as a flow diagram
We will now try to present the steps of the arithmetic coding procedure as a flow diagram. Let the alphabet of the message to be transmitted consist of the character set (in the examples above, this alphabet consisted of three characters,
, with i = 1 for
, i = 2 for
, and i = 3 for EOF). Construct an array of values
, where
is the relative frequency of the i-th character in the message. Let
= 0 and
, where N is the number of characters in the alphabet. (Again, in the coding example discussed above, we have
and
.) Using the notation thus introduced, the steps to be performed during arithmetic coding of each character can be presented as a flow diagram shown in Fig. 1.
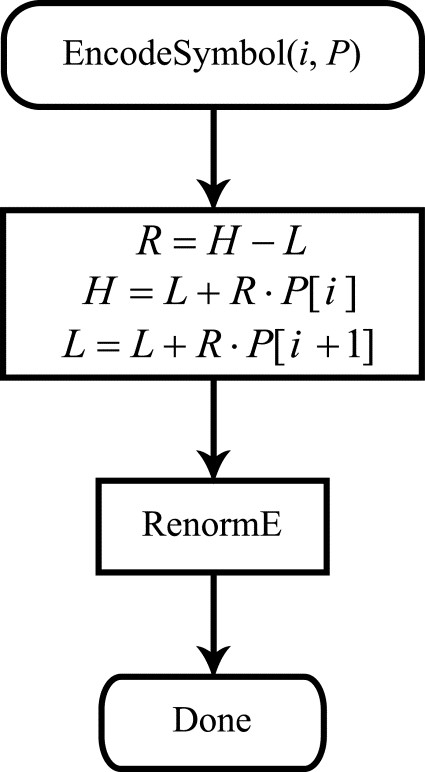
Figure 1. Flow diagram of the arithmetic coding procedure
The EncodeSymbol() procedure takes two arguments: i, the number of the character to be coded in the alphabet, and P, the array. As can be seen from the flow diagram, the first coding step consists of calculating the current interval length
(using the current values of the left and right interval endpoints,
and
respectively). The quantity
is used to calculate the updated values of the interval endpoints. Thus, in the first coding step for each message character, we split the current segment. The second step consists of a renormalization procedure, shown as a flow diagram in Fig. 2.
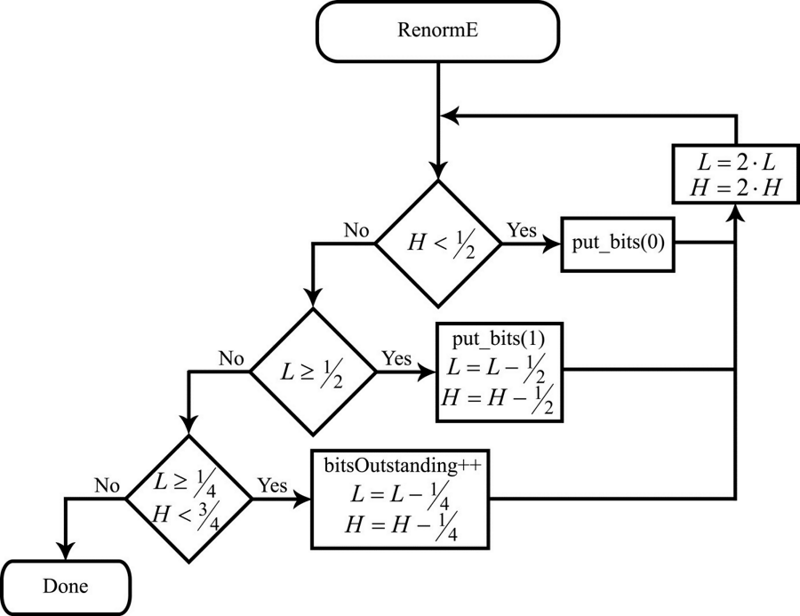
Figure 2. Flow diagram of the renormalization procedure
As already noted when discussing renormalization, if the current interval is fully contained inside the range [0, 1), i.e. if , a zero is output to the resulting bitstream followed by a sequence of ones equal in length to the value of the bitsOutstanding variable. All of this is carried out inside the put_bits() procedure, shown as a flow diagram in Fig. 4. The interval endpoint values
and
are doubled.
If the current interval is fully contained inside the range , i.e. if
, a one is output to the resulting bitstream followed by a sequence of zeros equal in length to the value of the bitsOutstanding variable (put_bits() is again used here). The interval endpoints in this case are modified so as to double the distance from
and
to 1. Therefore, the updated values of
and
can be calculated as:
,
,
which is carried out in this branch of the RenormE procedure.
Finally, if the current interval is fully contained inside the range , i.e. if
, and
, the value of bitsOutstanding is incremented by 1, and the interval endpoints are shifted towards each other so as to double the distance from
and
to
:
,
,
which is carried out in this branch of the RenormE procedure.
The flow diagram of the put_bits() procedure is shown in Fig. 4. This procedure takes the bit value (0 or 1) as an argument and outputs it to the resulting bitstream that represents the result of the arithmetic coding. The procedure of outputting the bit to the stream is designated as write_bit() in the flow diagram. After completing the output, the value of bitsOutstanding is checked. A sequence of !b values (here, the flow diagram uses the syntax for the Boolean NOT operation from the C language) equal in length to the value of bitsOutstanding is output to the bitstream.
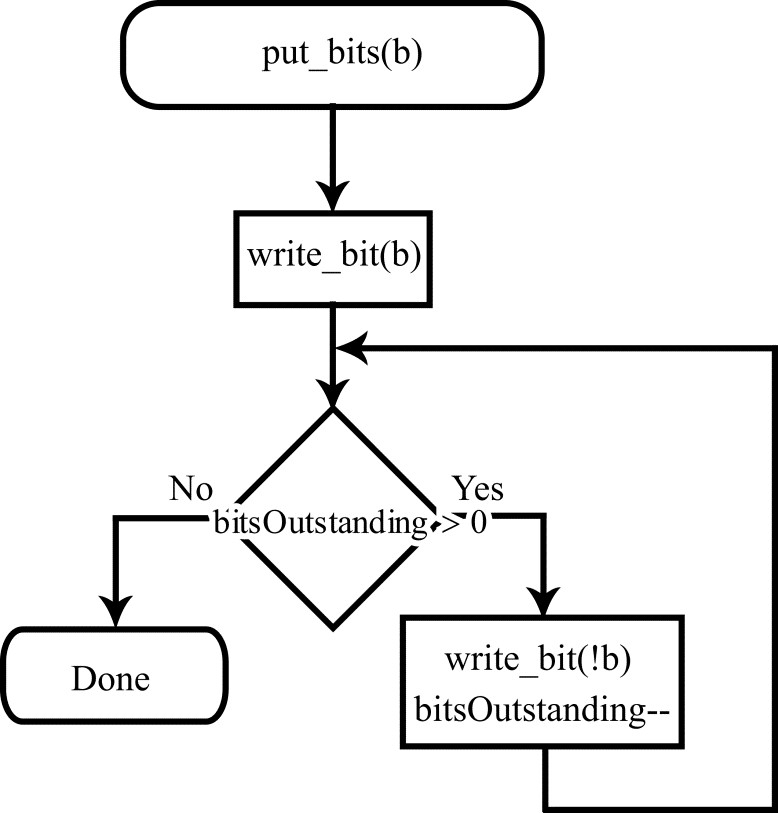
Figure 3. Flow diagram of the put_bits() procedure
June 13, 2019
Read more:
Chapter 1. Video encoding in simple terms
Chapter 2. Inter-frame prediction (Inter) in HEVC
Chapter 3. Spatial (Intra) prediction in HEVC
Chapter 4. Motion compensation in HEVC
Chapter 5. Post-processing in HEVC
Chapter 6. Context-adaptive binary arithmetic coding. Part 1
Chapter 8. Context-adaptive binary arithmetic coding. Part 3
Chapter 9. Context-adaptive binary arithmetic coding. Part 4
Chapter 10. Context-adaptive binary arithmetic coding. Part 5
About the author:
Oleg Ponomarev, 16 years in video encoding and signal digital processing, expert in Statistical Radiophysics, Radio waves propagation. Assistant Professor, PhD at Tomsk State University, Radiophysics department. Head of Elecard Research Lab.