ГЛАВА 11

Кратко о дискретном косинусном преобразовании и о том почему именно оно наиболее часто встречается в системах сжатия видеоизображений с потерями.
Перечислим еще раз основные этапы обработки видеокадра при кодировании системой стандарта H.265/HEVC (рис.1). На первом этапе (с условным названием «Разбиение на блоки») кадр разбивается на блоки CU (Coding Unit). На следующем этапе изображение внутри каждого блока предсказывается с использованием пространственного (Intra) или временного (Inter) предсказания. При выполнении временного предсказания блок CU может быть разбит на подблоки PU (Prediction Unit), каждый из которых может иметь собственный вектор движения. Значения предсказанных отсчетов вычитаются из значений отсчетов кодируемого изображения. В результате для каждого блока CU формируется разностный двумерный сигнал Residual. На третьем этапе двумерный массив отсчетов разностного сигнала разбивается на блоки TU (Transform Unit), которые подвергаются двумерному дискретному косинус-преобразованию Фурье (исключение здесь составляют блоки TU отсчетов яркости, полученные путем Intra-предсказания, размером 4x4, — для них используется дискретное синус-преобразование Фурье).
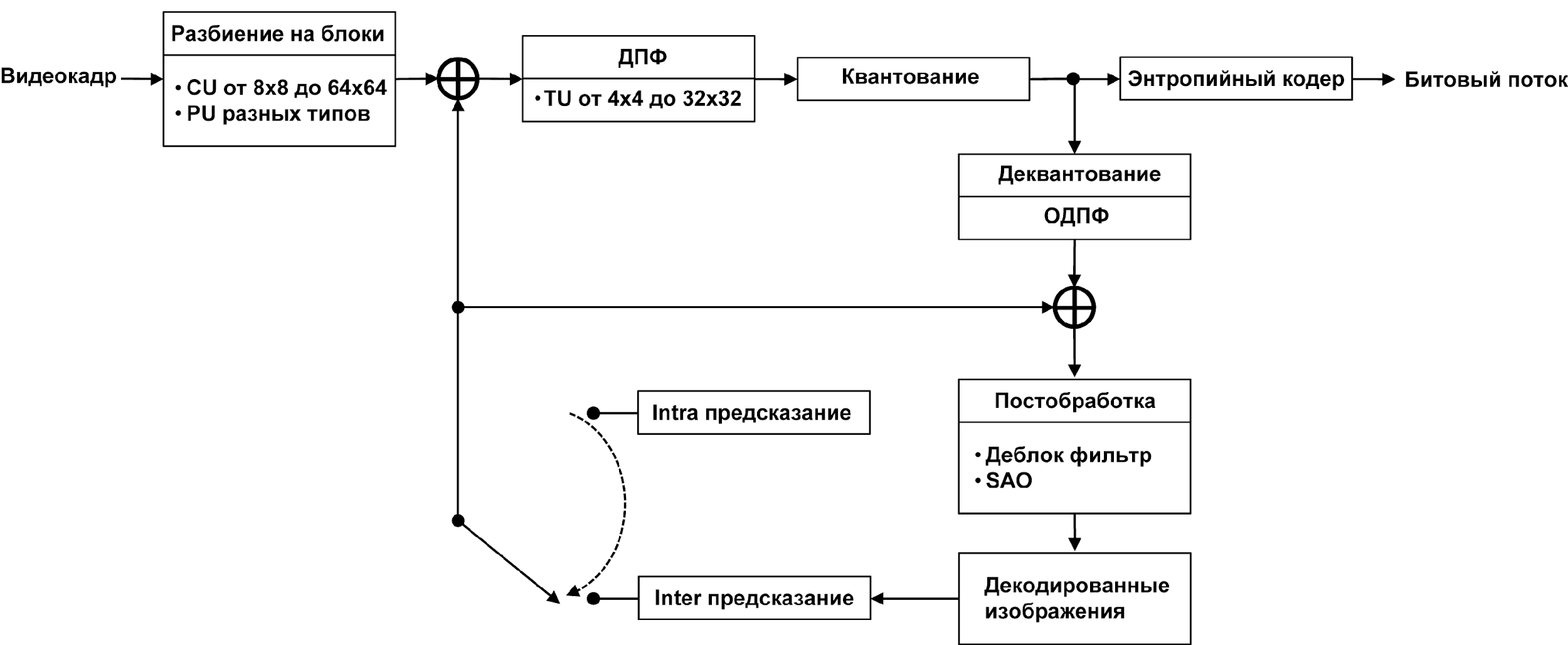
Рис. 1. Основные этапы кодирования видеокадра в системе стандарта H.265/HEVC
Затем спектральные Фурье-коэффициенты разностного сигнала квантуются по уровню. На последнем этапе информация о действиях, произведенных на всех четырех этапах, поступает на вход энтропийного кодера. Эта информация позволяет восстановить закодированное изображение. Здесь поступающие данные дополнительно сжимаются без потерь по алгоритмам контекстно-адаптивного двоичного арифметического кодирования (Context Adaptive Binary Arithmetic Coding, сокращенно CABAC).
В настоящей статье попробуем разобраться, что происходит с видеоизображением на третьем этапе сжатия. Почему на этом этапе используется дискретное косинусное (синусное) преобразование? Почему именно дискретное косинусное преобразование наиболее часто встречается в системах сжатия изображений (видеоизображений) с потерями (в таких системах на этапе сжатия в изображение вносятся искажения так, что декодированное изображение всегда отличается от оригинала)? Попробуем ответить на эти вопросы.
Почему именно дискретное косинусное преобразование наиболее часто встречается в системах сжатия изображений (видеоизображений) с потерями? Чтобы ответить на этот вопрос, необходимо обратиться к некоторым результатам теории случайных процессов. Эти результаты были первоначально получены Хоттелингом (Hotelling) (публикация 1933 г). Он предложил метод представления случайных процессов дискретного времени набором некоррелированных случайных коэффициентов. В 40-е годы 20-го столетия были опубликованы работы Карунена (Karhunen) и Лоэва (Loève), предложивших подобное представление для случайных процессов непрерывного времени. Сегодня в большинстве работ по цифровой обработке сигналов и дискретное, и непрерывное преобразования называют преобразованием Карунена-Лоэва или разложением по собственным векторам. Коротко представим здесь эти результаты, сразу ориентируясь на двумерный случай дискретного случайного процесса (изображения).
Преобразование Карунена-Лоэва описывается следующим соотношением:
\begin{array}{l}Y( u,v) =\sum ^{N-1}_{j=0} \ \ \sum ^{M-1}_{k=0} \ \ X( j,k) \ \ W( j,k,u,v),\\\end{array}
где $\displaystyle X(j,k) $ – дискретные отсчеты цифрового изображения, а ядро преобразования $\displaystyle W(j,k,u,v) $ удовлетворяет уравнению:
\begin{array}{l} \lambda ( u,v) W( j,k,u,v) \ =\ \sum ^{N-1}_{i=0} \ \sum ^{M-1}_{l=0} \ K( j,k,i,l) W( i,l,u,v),\\\end{array}
в котором за $\displaystyle K(j,k,i,l) $ обозначена ковариационная функция цифрового изображения, а $\displaystyle \lambda(u,v)$ при фиксированных значениях $\displaystyle u,v$ является константой. Как правило, считается, что ковариационная функция цифрового изображения $\displaystyle K(j,k,i,l) $ является разделимой, т. е. ее можно представить в виде произведения:
\begin{array}{l}K(j,k,i,l) =K_{C}(j,k)K_{R}(i,l),\\\end{array}
$\displaystyle K_{C}(j,k) $ - ковариационная функция изображения в вертикальном направлении ($\displaystyle j $ и $\displaystyle k $ являются номерами строк пикселов в изображении), $\displaystyle K_{R}( i,l)$ – ковариационная функция изображения в горизонтальном направлении ($\displaystyle i $ и $\displaystyle l $ являются номерами столбцов пикселов в изображении). В случае разделимости ковариационной функции ядро преобразования Карунена-Лоэва также является разделимым и преобразование можно выполнять сначала по столбцам пикселов, а затем по строкам (или наоборот). В этом случае ядро преобразования Карунена-Лоэва можно представить в виде:
\begin{array}{l}W\ ( j,k,u,v) \ =\ \ W_{C}( j,k) W_{R}( u,v),\\\end{array}
а каждый из сомножителей удовлетворяет своему уравнению:
\begin{array}{l}\lambda _{R}( v) W_{R}( i,v) =\sum ^{M-1}_{l=0} \ K_{R}( i,l) W_{R}( l,v),\\\end{array}
и
\begin{array}{l}\lambda _{C}( u) W_{C}( j,u) =\sum ^{N-1}_{k=0} \ K_{R}( j,k) W_{R}( k,u).\\\end{array}
Итак, преобразование Карунена-Лоэва позволяет представить цифровое изображение в виде набора некоррелированных случайных величин. И что в этом хорошего? Чем замечательно такое представление? Наиболее популярный ответ на эти вопросы содержится в книге «The Transform and Data Compression Handbook» (Ed. K. R. Rao and P.C. Yip. The Transform and Data Compression Handbook. Boca Raton, CRC Press LLC, 2001). В главе, посвященной преобразованию Карунена-Лоэва, авторы проводят следующий эксперимент. Они предлагают разбить изображение на неперекрывающиеся блоки, как показано на рис. 2 (взят из книги).
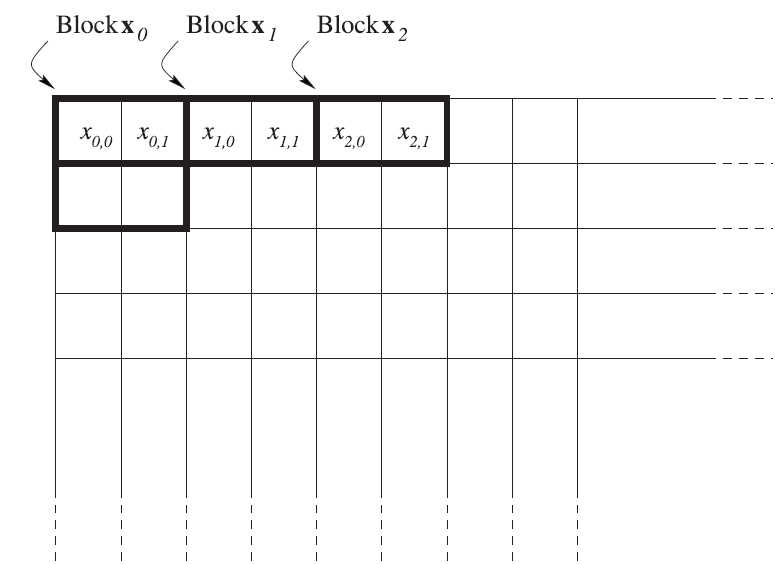
Рис. 2. Разбиение изображения на блоки
Весь набор блоков, очевидно, полностью определяет все обрабатываемое изображение. Таким образом, изображение оказывается представлено набором двумерных векторов $\displaystyle \overrightarrow{x_{i}} =(x_{i0},x_{i1})$ Диаграмма рассеяния всего набора векторов $\displaystyle \overrightarrow{x_{i}} $, на которой положения точек определяется координатами векторов $\displaystyle \overrightarrow{x_{i}} $ , представлен на рис. 3 (взят из книги).
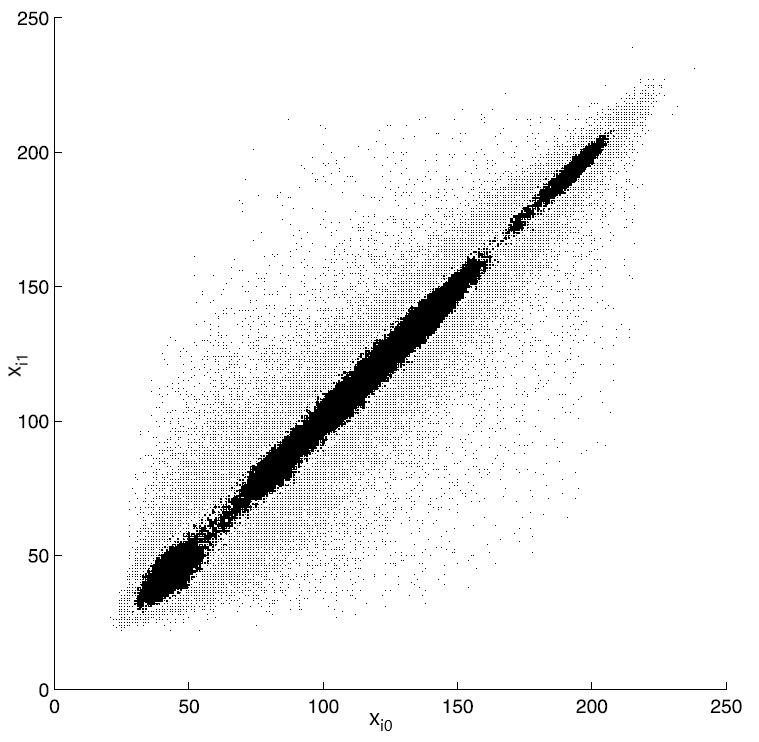
Рис. 3. Диаграмма рассеяния для векторов $\displaystyle \overrightarrow{x_{i}} $ .
Из диаграммы на рис. 3 видно, что значения соседних пикселов сильно коррелированы (хорошо просматривается прямая линия под 45 градусов на диаграмме). На рис. 4 (взят из книги) приведены гистограммы значений $\displaystyle x_{i0} $ и $\displaystyle x_{i1} $.
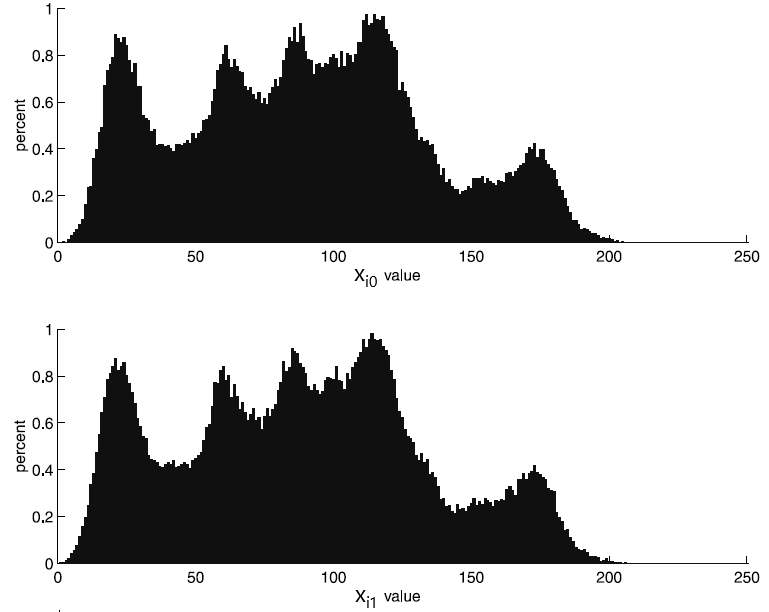
Рис. 4. Гистограммы значений пикселов $\displaystyle \overrightarrow{x_{i0}} $ и $\displaystyle \overrightarrow{x_{i1}} $
Преобразование Карунена-Лоэва преобразует векторы $\displaystyle \overrightarrow{x_{i}} $ в векторы $\displaystyle \overrightarrow{y_{i}} $ с координатами $\displaystyle ({y_{i0}},{y_{i1}}) $. Диаграмма рассеяния для векторов $\displaystyle \overrightarrow{y_{i}} $, приведенная на рис. 5 (взят из книги), демонстрирует отсутствие корреляции между координатами векторов $\displaystyle \overrightarrow{y_{i}} $.
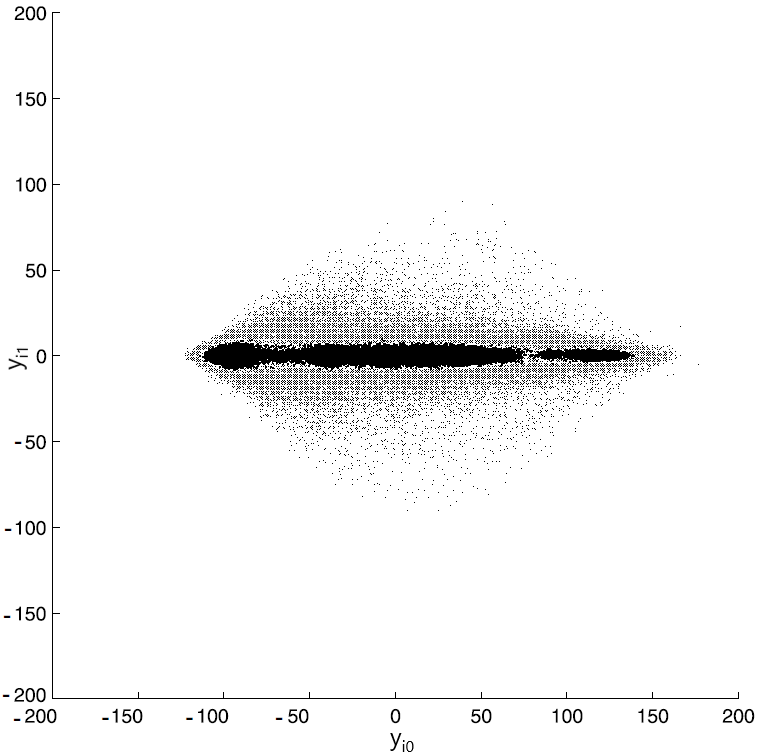
Рис. 5. Диаграмма рассеяния после преобразования Карунена-Лоэва
На рис. 6 (взят из книги) приведены гистограммы значений $\displaystyle y_{i0} $ и $\displaystyle y_{i1} $.
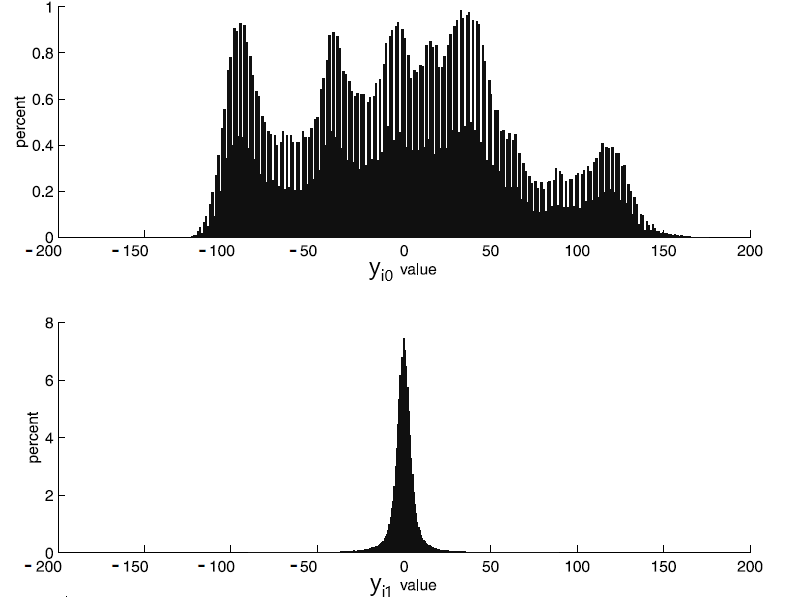
Рис. 6. Гистограммы значений координат векторов $\displaystyle \overrightarrow{y_{i}} $ .
Как видно из гистограммы, динамический диапазон значений $\displaystyle {y_{i0}} $ практически не отличается от исходного (диапазона значений $\displaystyle {x_{i0}} $). Диапазон же значений второй компоненты — $\displaystyle {y_{i1}} $ — изменился существенно. Гистограмма этой координаты в разы уже гистограммы $\displaystyle {x_{i1}} $. Очевидно, что чем меньше динамический диапазон какой-либо величины, тем меньшее количество бит необходимо для ее цифрового представления. Таким образом, даже в таком простом случае, когда преобразованию Карунена-Лоэва подвергаются двумерные векторы (а само преобразование сводится к повороту этих векторов на 45 градусов), оно обеспечивает сжатие изображения.
В более общем случае, когда векторы $\displaystyle \overrightarrow{x_{i}} $ имеют большую длину (как уже говорилось, при обработке изображений обычно предполагают, что двумерное преобразование Карунена-Лоэва разделимо и его можно выполнять последовательно в горизонтальном и вертикальном направлениях) их преобразование в векторы $\displaystyle \overrightarrow{y_{i}} $ с некоррелированными координатами обеспечивает большую степень сжатия. Более того, координаты векторов $\displaystyle \overrightarrow{y_{i}} $ оказываются наиболее устойчивыми к процедуре квантования. То есть, если мы квантуем коэффициенты разложения Карунена-Лоэва, а затем деквантуем их и выполним обратное преобразование, то ошибка, внесенная нами на этапе квантования, окажется минимальной из всех возможных линейных преобразований (минимальность ошибки здесь понимается в среднеквадратическом смысле). Также минимальную в среднеквадратическом ошибку среди всех линейных преобразований дает и откидывание некоторого количества последних коэффициентов (последних координат векторов $\displaystyle \overrightarrow{y_{i}} $). Таким образом, преобразование Карунена-Лоэва наиболее компактно размещает наибольшее количество информации, содержащейся в векторах $\displaystyle \overrightarrow{x_{i}} $ , в первых координатах векторов $\displaystyle \overrightarrow{y_{i}} $. Все это, конечно, делает преобразование Карунена-Лоэва практически идеальным для использования в системах сжатия цифровых данных и, в том числе, изображений.
Есть у преобразования Карунена-Лоэва один, но существенный, недостаток. Ядро преобразования определяется статистическим характером преобразуемых данных и для каждого набора векторов $\displaystyle \overrightarrow{x_{i}} $ требует решения приведенных выше уравнений. Аналитическое решение этих уравнений известно только в некоторых частных случаях. Численное решение возможно, но требует такого объема вычислений, что применение преобразования Карунена-Лоэва для обработки видеоизображений становится практически нереализуемым.
Одним из частных случаев случайных процессов, для которых известно аналитическое решение уравнений для ядра преобразования Карунена-Лоэва, являются марковские случайные процессы первого рода. У таких процессов при нормальном (гауссовом) распределении значений корреляционная функция имеет показательный характер. Для дискретного одномерного случайного процесса корреляционная функция $\displaystyle K(i,j) $ имеет вид:
\begin{array}{l}K( i,j) \ =σ^{2} ρ^{|i-j|},\\\end{array}
где $\displaystyle 0\leqslant ρ \leqslant 1$. В работе «Relation between the Karhunen Loeve and cosine transforms» (RJ. Clarke, B.Tech., M.Sc, C.Eng., Mem.I.E.E.E., M.I.E.E. Relation between the Karhunen Loeve and cosine transforms. IEEPROC, Vol. 128, Pt. F, No. 6, NOVEMBER 1981) показано, что при $\displaystyle ρ → 1$, решение, полученное для марковского процесса, совпадает с дискретным косинусным преобразованием Фурье 2-го типа (как известно, всего существует восемь типов дискретного косинусного преобразования Фурье). С другой стороны, многочисленные исследования статистических свойств цифровых изображений показали, что корреляционные функции изображений в горизонтальном $\displaystyle K_{R}(i,j) $ и вертикальном $\displaystyle K_{C}(i,j) $ направлениях имеют показательный вид. Значения $\displaystyle ρ$ при этом в обоих направлениях близко к 1 (составляет 0.95–0.98). Таким образом, для большинства изображений преобразование DCT-II является очень хорошей аппроксимацией преобразования Карунена-Лоэва, а ядра преобразования в горизонтальном и вертикальном направлениях имеют одинаковый вид:
\begin{equation*} W( i,k) =\begin{cases} \frac{1}{\sqrt{N}} & i=0,\ 0\leqslant k\leqslant N-1\\ \sqrt{\frac{2}{N}}\cos\left(\frac{i\pi ( 2k+1)}{2N}\right) & 0< i\leqslant N-1,\ 0\leqslant k\leqslant N-1 \end{cases} \end{equation*}
Вернемся теперь к первому вопросу, заданному в начале статьи.
Почему на третьем этапе используется дискретное косинусное (синусное) преобразование? Почему используется дискретное косинусное преобразование — понятно. Это преобразование является хорошей аппроксимацией преобразования Карунена-Лоэва для большинства изображений (в том числе и изображений, получаемых после выполнения Inter-предсказания, т. е. для разностного сигнала). А откуда взялось синусное преобразование?
Еще в самом начале разработки стандарта HEVC научная группа из Сингапура (Document: JCTVC-B024) показала, что корреляционные свойства разностного сигнала, получаемого при Intra-предсказании, существенно отличаются от корреляционных свойств обычных изображений и свойств разностного сигнала, получаемого при межкадровом предсказании. Это легко понять. Действительно, отсчеты разностного сигнала, находящиеся наиболее близко к референсным отсчетам, используемым при Intra-предсказании, очевидно обладают наименьшей дисперсией. По мере удаления отсчетов разностного сигнала от референсных дисперсия нарастает. Ученые из Сингапура получили аналитическое выражение для корреляционной функции разностного сигнала при горизонтальном и вертикальном направлениях Intra-предсказания. Ими же было показано, что ядром преобразования Карунена-Лоэва в этих случаях является функция:
\begin{array}{l}W( i,j) =\frac{2}{\sqrt{2N+1}}\sin\frac{\pi ( 2i+1)( j+1)}{2N+1} ,\ 0\leq i,j\leq N-1\\\end{array}
которая совпадает с ядром синусного дискретного преобразования Фурье.
9 апреля 2021
Читать другие статьи:
Глава 1. Просто о видеокодировании
Глава 2. Межкадровое (Inter) предсказание в HEVC
Глава 3. Пространственное (Intra) предсказание в HEVC
Глава 4. Компенсация движения в HEVC
Глава 5. Постпроцессинг в HEVC
Глава 6. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 1
Глава 7. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 2
Глава 8. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 3
Глава 9. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 4
Глава 10. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 5
Автор:
Олег Пономарев - 17 лет занимается вопросами видео кодирования и цифровой обработки сигналов, специалист в области распространения радиоволн, статистической радиофизики, доцент кафедры радиофизики НИ ТГУ, кандидат физико-математический наук. Руководитель исследовательской лаборатории Elecard.
Инструмент для детального анализа этапов кодирования видеопоследовательности - Elecard StreamEye
Инструмент для сравнения параметров видео, закодированного разными энкодерами